·
Daily
using of ABC Forth
Ching-Tang Tseng
Hamilton, New Zealand
1
March 2017
ilikeforth@gmail.com
http://forthfortnight.blogspot.com
This article shows a few examples
to you. Let you know how to purify a little bit confused question by ABC Forth
system? Questions are coming from other people's posting on my Face Book
website. I owned ABC Forth for many years, could be applied to solve these
kinds of question.
Many years ago, I had ever
struggled for a long period of time, try to set up some questions by myself,
would like to use them to evaluate my ABC Forth system. Recently, on Face Book,
I found many current questions are good to be used to show the special
performance of my ABC Forth. I implement these programs on 64 bits ABC Forth system
under ubuntu 16.04 OS. I am sure all high school students are able to
understand the following demonstration by themselves directly.
All questions are analyzable
problem. You are able to inference out their answers by hand. I prefer to solve
them with computer program. ABC Forth has been emphasized on purpose.
(1). This question is showing clear enough in
mathematic expression.
BRILLIANT.ORG
\ ABC FORTH demo code
\ Author : Ching-Tang Tseng, Hamilton NZ
\ Date : 1
March 2017
\ Contact : ilikeforth@gmail.com
\ Website : http://forthfortnight.blogspot.com
4 integers i j x y
: x+y=? ( -- )
basic
10 for i = -100 to 100
20 for j = -100 to 100
30 let x = i
40 let y = j
50 if ( abs ( x ) + x + y = 8 )
and ( x + abs ( y ) - y = 14 ) then 70
60 goto 80
70 print " x = " ; i , " , y = " ; j , " , x + y = " ; i + j
80 next j
90 next i
100 end ;
basic
10 for i = -100 to 100
20 for j = -100 to 100
30 let x = i
40 let y = j
50 if ( abs ( x ) + x + y = 8 )
and ( x + abs ( y ) - y = 14 ) then 70
60 goto 80
70 print " x = " ; i , " , y = " ; j , " , x + y = " ; i + j
80 next j
90 next i
100 end ;
\ execution result:
\ x+y=?
\ x = 6 , y = -4 , x + y = 2 ok
\ x = 6 , y = -4 , x + y = 2 ok
The most special part in this program is the logic branch
expression almost the same as the question described.
(2)
2.1 Question: How many squares are in
the 20th figure?
According to increase
a fixed amount of squares each time, appending them all together, to form an extensible figure.
How many squares are
present in figure number i?
Figure shows that increased
fixed amount is 4, suppose i-th step gets k squares.
While i = 1 , k(1) =
1
While i = 2,3,...n,n+1,
k(n+1) = k(n) + 4
2.3 Program
2 integers i k
: test ( -- )
basic
10 let k = 1
20 print " i = 1 k = 1 "
30 for i = 1 to 20 - 1
40 let k = k + 4
50 print " i = " ; i + 1 , " k = " ; k
60 next i
70 end ;
2.4 Execution results
test
i = 1 k = 1
i = 2 k = 5
i = 3 k = 9
i = 4 k = 13
i = 5 k = 17
i = 6 k = 21
i = 7 k = 25
i = 8 k = 29
i = 9 k = 33
i = 10 k = 37
i = 11 k = 41
i = 12 k = 45
i = 13 k = 49
i = 14 k = 53
i = 15 k = 57
i = 16 k = 61
i = 17 k = 65
i = 18 k = 69
i = 19 k = 73
i = 20 k = 77 ok
Then, answer is 77.
2.5 Discussion
There is always a
formula existed if a mathematical question is an analytic problem.
A very simple
regulation is very easy to be find out from the figure above.
This is its corresponding
mathematical expression formula:
k = ( i - 1 ) * 4 + 1
, i = 1, 2, 3, ........, n
If we are insisted to
have pure FORTH style program only. It will be more simpler as following:
: test ( i -- k )
1- 4 * 1+ ;
Execute 20 test, you
are getting 77.
(3)
3.1 Question:What does this simplify to?
3.2 Description
This question is been used to
let the student practice how to simplify a mathematical expression. It is not
for calculation practice.
ABC Forth deal with the
operation precedence systematically. So long as the user didn't violate the writing
regulation of traditional mathematical requirement, system output certainly should be correct.
In ABC FORTH system, you are permitted to use infix
style only to design your program. There is no restriction on must to be BASIC
style. Which style you are preferred is fully up to you.
ABC Forth divided the using
environment between integer number and floating point number rigorously. You
are not allowed to mix both of them together, but indexes in array or in matrix
should be integer.
Then, this question list above,
we are able to prove its result by two kinds of number format. Original mathematical
expression has exponent, square root, multiplication operations. According to
the question, it must be written as the following format. This format is almost
the same as the traditional fundamental hand writing format. It is apt to write,
apt to check, apt to remember and apt to understand.
Executed the final program to
get the answer, we found out the first one of 4 options is our answer, all
others are wrong. This special application is one kind of ABC Forth application.
3.3 Program
2
reals x y
:
RTest
( f -- )
{{ x }} f! {{ y = 0 }}
{{ y = sqrt ( 2 ^ ( sqrt ( 4 * x * x ) ) ) }}
y f. ;
2
integers a b
:
ITest ( n -- )
[[ a ]] !
[[ b = sqrt ( 2 ^ ( sqrt ( 4 * a * a ) ) ) ]]
b . ;
3.4 Execution results
3.e0
RTest 8.00000 ok
3
ITest 8 ok
When
X = 3, 2 ^ X = 2 ^ 3 = 8, question to be proved.
3.5 Discussion
In programming phase, if you are
unable to make sure that your operation precedence arrangement are exactly
right, the simplest solving method is to use many pairs of ( ... ) in your
expression. Parentheses' mark own the top most precedence in ABC Forth system.
(4)
4.1 Question:Can you solve for x?
4.2 Description
In general, traditional
programming language did not supply factorial operator ( ! ) to user. There are
two reasons:
First reason, it is available in positive
integer only, using range are very narrow. For a 32 bits system, the maximum
integer should be less than 13. You have to take care these factors, if using
it in your program.
The following program tells you
this restriction directly, beware the output results beyond integer 13.
2 integers i j
: test ( -- )
basic
10 let j = 1
20 for i = 1 to 20
30 let j = j * i
40 print i , j
50 next i
60 end ; ok
test
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
10 3628800
11 39916800
12 479001600 <--- upper limit is 12
13 1932053504
14 1278945280
15 2004310016
16 2004189184
17 -288522240
18 -898433024
19 109641728
20 -2102132736 ok
-1 1 rshift . 2147483647 ok
Secondary reason, if we consider
factorial operator ! is a mathematical function as well, his writing position
is totally different from all other operators. Four arithmetical notations +,-,*,/
are infix operators. General functions, for examples, sin, cos, tan, exp, ln
... etc, are prefix operators. Only factorial notation ! is a postfix operator.
In expression, it is to be written as 7 ! such a format.
FORTH is a standard postfix
programming language. To design such a function into FORTH is very easy. In
BASIC style environment, we must consider the problem of how to mix a single postfix
operator with all other non-postfix operators. In ABC Forth, this problem is
resolved by precedence arrangement. You are permitted to write factorial
operator in your program totally the same as in your arithmetical book.
Then, the program for this
question could be designed almost the same as what the question is asking?
4.3 Program
\ ABC FORTH can implement this code out directly.
\ If rewrite 20 let x = 14, it will tell you that system is running out of
range.
\ It means that solution is exited and x = 12 is an unique solution.
integer x
: test ( -- )
basic
10 let x = 0
20 let x = x + 1
30 if ( x ! + 11 ! + 10 ! ) / ( 7 ! * 5 ! * 3 ! ) = x * x then 50
40 goto -20
50 print " x = " ; x
60 end ;
4.4 Execution results
test
x = 12 ok
4.5 Discussion
Owing to FORTH language is a
natural integer programming language. It means that FORTH is good for solving
all integer problem. In 64 bits FORTH, there are 19 digits integer range could
be used. Factorial values from 1 to 30 are showing here.
\ 64 bits factorial !
2 integers i j
: test ( -- )
basic
10 let j = 1
20 for i = 1 to 30
30 let j = j * i
40 print i , j
50 next i
60 end ; ok
test
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
10 3628800
11 39916800
12 479001600
13 6227020800
14 87178291200
15 1307674368000
16 20922789888000
17 355687428096000
18 6402373705728000
19 121645100408832000
20 2432902008176640000
21
-4249290049419214848 <--- out of
64 bits integer range
22
-1250660718674968576
23 8128291617894825984
24
-7835185981329244160
25 7034535277573963776
26
-1569523520172457984
27
-5483646897237262336
28
-5968160532966932480
29
-7055958792655077376
30
-8764578968847253504 OK
-1 1 rshift .
9223372036854775807 OK
5.2 Description
Ok, let's don't use calculator, let's
divert to use computer. The difference of using between these two devices are:
Calculator doesn't need too much
thinking, needs pushing down its keys many times.
Computer needs some thinking and
must find out general expressions before you are coding the program.
This question is asking you to deal
with summation of one set of series. Before coding, we need to sort out so called
general expression. They are combined with two simple terms.
n ^ 2 - ( n - 1 ) ^ 2
Then, the program could be
coded out directly. This is the procedure what I did.
5.3 Program
2 integers y i
: Answer ( -- )
basic
10 let y = 0
20 for i = 100 to 1 step -2
30 let y = y + i * i - ( i - 1 ) * ( i - 1 )
40 next i
50 print " Sum = " ; y
60 end ;
5.4 Execution Results
Answer
Sum = 5050 ok
5.5 Discussion
Overflow is always the most
serious nightmare to all programmer. According to the general expression above,
we could checked it out, one term is addition, another one term is subtraction.
They are compensated each other, so we are able to ignore the overflow problem.
(6)
6.1 Question: Can you find n?
6.2 Description
Questions above talked a lot
already. No more comment here.
6.3 Program
integer
n
:
FindN ( -- )
basic
10
let n = 0
20
let n = n + 1
30
if n + n ^ 2 + n ^ 3 + n ^ 4 = ( n + 2 )
! then 50
40
goto -20
50
print " n = " ; n
60
end ;
6.4 Execution results
FindN
n
= 3
6.5 Discussion
Iteration incremental amount in program is
no upper limit. I let it begin from 0, owing to the answer is impossible to be a
negative number. You are unable to get the answer intuitively, so I wrote this
program.
My daily thinking today:
Every year, close to 28th February, the current Taiwan government is always sly to cheat all people with something about 228 affairs.
What does '228 affairs' mean?
After World War II, Japan surrender to China, but China government had never asked all Japanese to depart out from Taiwan. Roughly said, over that time, there were about 800 thousand Japanese resident in Taiwan still.
Kindly attitude from Chinese to Japanese had never been fed back any make sense response from Japanese all the time. Instead of such a Chinese kindness to Japanese, many terrible things happened to us in Taiwan after the time of Japan surrender to China.
It was a terrible affair occurred in Taiwan on 28th February 1947. Many successor of Japanese and their stupid follower, communists, and a lot of rubbish people made a comprehensive turmoil in Taiwan.
During the turmoil period of time, there were many people, they are come from Mainland China later, had been killed randomly. Turmoil people robbed weapons from army, occupied government's building as well.
Under such a situation, China government had no choice, military suppress happened, about 600 Taiwanese turmoil people were killed on site in those turmoil affairs, and more than thousand uncountable people come from Mainland China later were killed by turmoil Taiwanese.
The current Taiwan government are organized by folks pigs of Japanese. They used cheating method in national election took over the government. For the present in Taiwan, talking about the people come from Mainland China had been killed in 228 affairs in public site are prohibited. But those 600+Taiwanese victim family of 228 affairs had got huge compensation money from government already. Some of them are pseudo victims.
This is the true fact of 228 affairs in Taiwan.
Let's tell one true thing had ever happened in 228 affairs.
One person name Liu Chin San. In 1947, he was one of the people come from Mainland China later in Taiwan.
Before 228 affairs, he was one staff worked for a government company to manage exclusive cigarette and liquor.
After 228 affairs happened, one day, he had been hurt under a horrible condition, and had been sent to hospital in Taichung city.
The following day, those hurt Liu's turmoil Taiwanese heard that Liu didn't died and still alive in the hospital. Those turmoil Taiwanese rushed to the hospital immediately and killed Liu in the ward with more terrible actions, cut his ears down and dug his eyes out.
This terrible thing had ever been reported on many newspaper. And there was still a government file recorded that government company had ever arranged Liu's funeral ceremony.
The current Taiwan government would like to cheat everybody with something about 228 affairs. I'd like to tell something of the truth to all of the world.
228 affairs was an interior affairs of China government dealt with Taiwan turmoil. It was not a terrorists attacked events.
二二八真相
二二八期間,台中瘋狂打殺外省人,公賣局專员劉青山被打成重傷住院。第二天暴徒聽說劉青山没死,他们衝到病床前把劉青山打死。割掉耳鼻,挖掉双眼。
劉青山案相關挡案很多,许多报纸报導外,挡案中还有公卖局替劉青山辨公祭的资料。
三月二十五号,台湾已經平静,但是不少外省人夜宿碼頭急着逃離台湾,可見外省人惊恐到什麽程度。
民進党天天吵着要真相,现在我㑹不停地告訴你們真相。
Announcement to all of the world:
Everybody should know the real historical fact. The territory of Japan should be shrunken to three islands as the following map displayed.
In historical fact, more than 36 sequential islands of Okinawa was Chinese territory originally,
American did the bad arrangement on purpose, let it occupied by Japanese after World War II.
There was a nation organized by the aboriginal people named Ar-yi-nu kingdom on whole Hokkaido island.
Japanese killed almost all aboriginals on this island and occupied it.
附註 : 20241031 重新整理後貼出。
(7)
7. 1 Question: Your calculator probably won't help you here...
My suggestion: ABC
FORTH can help you some.
7. 2 Description
Yes, general calculator indeed won't help you to solve this
question. Even more remarkable, a 64 bits general FORTH system won't help you
as well.
Big number operation functions had been built in ABC FORTH
system. You are able to code the big number in the program. Let the system
tell you the result.
Besides, we are able to solve this problem by using floating
number operation, convert numbers back and forth by two logarithmic functions Log
and ALog.
So long as you are able to get two values in your program, compare both of them is simple and directly.
7.3 Program
16 bigvariable a 20 allot
17 bigvariable b 20 allot
: test1 ( -- )
basic
10 let B{ a = a ^ 17 }B
20 let B{ b = b ^ 16 }B
30 if B{ a > b }B then 60
40 print " 17 ^ 16
> 16 ^ 17 "
50 goto 70
60 print " 16 ^ 17
> 17 ^ 16 "
70 run cr ." 16 ^ 17 = " a big.
80 run cr ." 17 ^ 16 = " b big.
90 end ;
2 reals x y
: test2 ( -- )
basic
10 let { x = alog ( 17 * log ( 16 ) ) }
20 let { y = alog ( 16 * log ( 17 ) ) }
30 if { x > y } then 60
40 print " 17 ^ 16
> 16 ^ 17 "
50 goto 70
60 print " 16 ^ 17 > 17 ^ 16 "
70 print " 16 ^ 17
= " , { x }
80 print " 17 ^ 16
= " , { y }
90 end ;
7.4 Execution Results
test1
16 ^ 17 =
21 digits
295147905179352825856
17 ^ 16 =
20 digits
48661191875666868481
test2
16 ^ 17 > 17 ^ 16
16 ^ 17 =
2.95148E20
17 ^ 16 =
4.86612E19 ok
7.5 Discussion
There are two purposes to list this big number program here:
First, it demos out the big number operation performance that general
system is not so easy to possess. Second, it could print out the absolute value of a big number.
16 to the power of 17 is a 21 digits value. In 64 bits forth
system, a maximum single integer number is a 19 digits number only. In this
question above, we have got this hint already.
Owing to the big number coding format does not have a
programming standard. ABC FORTH built a few fundamental functions inside independently.
There are some restrictions for using. You are rarely able to find this kind of program from other places. My personal programming style is served to you for
reference only.
Stack variation indication can tell you how does big** function worked in the system.
big** ( addr1 n -- addr2 )
addr1 is the initial address of a base big number, n is its integer
power, addr2 is the initial address of the calculation result big number.
To claim out a structure for a big number, please use this
format:
n1 bigvariable <name> n2 allot
stack variation indication of a bigvariable is as following:
bigvariable ( n --
) compiling time
( --
addr ) interpreting time
n1 is the initial value of a big number. It must be a reasonable integer,. <name> is an up to you given name of
this big number. n2 is the needed memory amount to ALLOT.
Usage principle of n2 is depended on how many digits does this big
number required? Then, ALLOTs out the same amount bytes for it. In fact, we need
80% bytes memory amount only. Here we use 20 in the program.
Specification of a big number output instruction is Big.
Big. ( addr -- )
addr is the initial address of a big number.
Direct operate the intrinsic words in this big number included
system, you are able to get the calculation result by a big number operation as
following:
big 16 17 big** big.
21 digits
295147905179352825856 ok
The difference between direct operation mode and programming
mode is that the former direct operation mode is eating memory each time or say that
it is a memory hungry operation mode.
The latter programming mode has no memory hungry problem.
After you compile a big number program, no matter how many times you have done to execute it, ABC FORTH system is always keeping the memory consuming amount 0.
A few big number words are introduced here only.
(8)
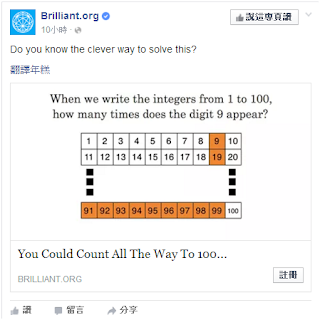
8.1 How many times does the digit 9 appear?
8.2 Description
Obviously, It is not an intelligent idea to solve this question by
computer program. But versatility of a program has its advantage relative to
other methods. Appropriate program could be applied to all conditions by
adjusting parameters.
Number to be thought as characters is one dealing with method. Number to
be thought as value is another method to deal with. We are using ABC FORTH
mathematical calculation system, so the latter method are preferred. We think
number as a value.
In all FORTH system, there is a special instruction named MOD existed. MOD
can help us to get the remainder after a division operation. To get value 9 by
division is the key procedure in the program.
There is a trick in the following program line label 20. Owing to the
FOR instruction in ABC FORTH system is formed by LET instruction. Both
instruction's position could be replaced by each other. I would like to show
you this performance only. Base on the fundamental principle, to let you apt to
maintain your program in future. My suggestion is still don't ignore FOR from
system. FOR ... NEXT pair makes reading of program more clear.
8.3 Program
2
integers count i
:
test ( -- )
basic
10
let count = 0
20
let i = 1 to 100
30
if i mod 10 = 9 then 50
40
goto 60
50
let count = count + 1
60
if i / 10 = 9 then 80
70
goto 90
80
let count = count + 1
90
next i
999
print count
1000
end ;
8.4 Execution Results
test
20
ok
8.5
Discussion
Here is another program to be implemented by GOSUB ... RETURN pair.
Function of this program is thoroughly the same as the program listed above.
But in fact, in ABC FORTH system, there is another very powerful special
instruction, named RUN, able to execute any one word or words out of a defining
word's range. GOSUB ... RETURN could be fully ignored under such a situation.
We keep GOSUB ... RETURN pair in the system for convenience.
:
test ( -- )
basic
10
let count = 0
20
let i = 1 to 100
30
if i / 10 <> 9 then 50
40
gosub 500
50
if i mod 10 <> 9 then 70
60
gosub 500
70
next i
80
goto 999
500
let count = count + 1
501
return
999
print count
1000
end ;
test
20
ok
(9)
9.1 Question: What is the limit?
9.2 Description
L'Hopital's rule should be the formal application for such a question. You
are able to learn this rule from an elementary calculus course.
Here, I submit another flavor of solving method. Let the computer program
tells you the limit by numerical analysis method.
Analytic method is given by this procedure: execute differential operation once for both of
numerator expression and denominator expression, substituted 1 into x, then get
answer = 15 / 10 = 3 / 2 = 1.5.
Programming method has no differential treatment inside. We substitute into
x with a few real values directly. Values are from a little bit bigger than 1
converged to 1 step by step. Then print out a series of numerical calculation
results in sequence. You are able to see the last value in this output listing
will be the same answer value as talked above in analytic method.
9.3 Program
4
reals x y f1 f2
:
test ( -- )
basic
10
let { y = 1 }
20
let { y = y / 10 }
30
let { x = 1 + y }
40
if { x <= 1 } then 90
50
let { f1 = x ^ 15 - 1 }
60
let { f2 = x ^ 10 - 1 }
70
print { x , f1 / f2 }
80
goto -20
90
end ;
9.4 Execution Results
test
1.100000000000000
1.993576910297222
1.010000000000000
1.538574701453724
1.001000000000000
1.503760637188892
1.000100000000000
1.500375106262153
1.000010000000000
1.500037501059981
1.000001000000000
1.500003749983436
1.000000100000000
1.500000374700102
1.000000010000000
1.500000037747582
1.000000001000000
1.500000000000000
1.000000000100000
1.500000000000000
1.000000000010000
1.500000000000000
1.000000000001000
1.500000000000000
1.000000000000100
1.500000000000000
1.000000000000010
1.500000000000000
1.000000000000001
1.500000000000000 ok
9.5 Discussion
Implementation is the best proof for testing of a theory.
(10)
10.1 Question: How big can N be?
10.2 Description
this is a question of inequality equation. Replace greater than mark >
by equal sign =, we are able to compute out what is the maximum value of this
equation.
In the expression, a standard floating point number function of logarithm
has been used. If N is to b restricted should be an integer, then mixing operation of
integer number and floating point number must to work together effectively in
the program. ABC FORTH permits you to do these kinds of arithmetical operation.
10.3 Program
integer
n
:
test1 ( -- )
basic
10
let n = 0
20
let n = n + 1
30
if { ( log 10 + log 20 ) > ( 2 * log ( i>r ( n ) ) ) } then -20
40
print " max n = " , n - 1
50
end ;
:
test2 ( -- )
basic
10
print " max n = " ; { alog ( (
log 10 + log 20 ) / 2 ) }
20
end ;
10.4 Execution Results
test1
test2
max
n = 14
max
n = 14.14213562373095 ok
10.5 Discussion
Except integral index of an array or of a matrix, any one integer
number should be converted into a floating point number format first, before it
can be used in the floating point algebraic expression programming environment.
Converting instruction I>R is working totally the same as a general
mathematical function do.
Program are translating arithmetical expression into the domain
of logical branch condition only. Flowing stream line of program will be guided
by this logical branch.
We are going to get the maximum value. Let program started by guess
from the smallest value 0. Let value keep going to increase 1 each time while
the logical condition is true, until it is failed, that value minus 1 will be
the answer.
The same meaning, equal equation with maximum value, expressed
as in program test2, will give you the real number answer.
Submit such a topic has another purpose. Logarithmic formulas such
as following
Log A*B = Log A + Log B 、 Log A/B = Log
A - Log B ...etc.
are not so easy to remember all of them. Even me, especially
when I am getting old gradually, it is more difficult to remember as well.
Solving such a question can help us to remember Logarithmic formulas.
Solving such a question can help us to remember Logarithmic formulas.
Similarly, if the base of a Logarithm is not 10, for example to be changed to 2, expressed as following
Ln(2) 8 = n, or Ln_2 8 =
n, or Lb 8 = n
Its directed meaning is
2 ^ n = 8
2 ^ n = 8
Remember this relationship with such an expression can help you everywhere to operate Logarithm function more convenient.
(11)
11.1 Which one do you think is bigger?
11.2 Description
It is impossible to get the exact value of 300 ! in a general FORTH
system, except you added big number instructions to it. It has been told that
for a 32 bits system, the cover range of a single integer should be less than 12 !. Even
though you are able to use floating point function, for an 8 Bytes/Float
condition, value of 300 ! is still overflow out of the upper limit 10 to the power
of 308, system will warning you: it is 'infinite!'. 10 Bytes/Float format floating
point number functions are able to cover the value of 300 !.
ABC FORTH possesses 10 Bytes/Float performance to compute 300 ! directly.
Owing to the accumulated error in 300 times computation and inevitable number formats convert, the result value will be last 2 digits inaccuracy. You are able to find it
out by compare. please refer to the listing of this big number value in 11.5
11.3 Program
INTEGER
I
2
REALS X Y
:
TEST ( -- )
BASIC
10
LET { X = 300 ! }
20
LET { Y = 1. E 0 }
30
FOR I = 1 TO 300
40
LET { Y = Y * 1. E 2 }
50
NEXT I
60
IF { X > Y } THEN 90
70
PRINT " 100^300 > 300! "
80
GOTO 100
90
PRINT " 300! > 100^300 "
100
PRINT { " 300! = " ; X }
110
PRINT { " 100^300 = " ; Y }
120
END ;
11.4 Execution Results
TEST
300!
> 100^300
300!
= 3.0605751221644063616 E 614
100^300
= 1. E 600 OK
11.5 Discussion
Two programs compute out the value of 300 ! directly. All big number
operations are running continuously in the program.
2
INTEGERS I N
0
BIGVARIABLE X
0
BIGVARIABLE Y 40000 ALLOT
:
BIG!. ( n -- )
[[
N ]] !
BASIC
10
LET B{ X = BIG0 }B
10
LET B{ Y = BIG1 }B
20
FOR I = 1 TO N
30
LET B{ X = X + BIG1 }B
40
LET B{ Y = Y * X }B
50
NEXT I
60
RUN Y BIG.
70
END ;
or
:
BIG! ( n -- addr )
[[
N ]] !
BASIC
10
LET B{ X = BIG0 }B
10
LET B{ Y = BIG1 }B
20
FOR I = 1 TO N
30
LET B{ X = X + BIG1 }B
40
LET B{ Y = Y * X }B
50
NEXT I
70
END
B{{
Y }}B ;
Execute 300
BIG!. get
615
digits
30605751221644063603537046129726862938858880417357
69994167767412594765331767168674655152914224775733
49939147888701726368864263907759003154226842927906
97455984122547693027195460400801221577625217685425
59653569035067887252643218962642993652045764488303
88909753943489625436053225980776521270822437639449
12012867867536830571229368194364995646049816645022
77165001851765464693401122260347297240663332585835
06870150169794168850353752137554910289126407157154
83028228493795263658014523523315693648223343679925
45940952768206080622328123873838808170496000000000
00000000000000000000000000000000000000000000000000
000000000000000 ok
Simple
floating point number computational result is listed here again, please compare it
with the listing above.
300!
= 3.0605751221644063616 E 614
There
are two closed words named BIG!. and BIG! to be used as the name of each
program. Differences are to be arranged
on output interface places only. Latter one program could be cited by other advanced
using in this system. This is an intrinsic characteristic of FORTH.
(12)
12.1 Question: Find the last digit.
12.2 Description
This is another question it results overflow problem in 32 bits system.
Let us print out the square value of each integer in sequence first.
6
integers i j k l p s
:
demo (
n -- ) \ maximum < 11
[[
j ]] !
basic
10
let k = 0
20
for i = 1 to j
30
print " " ; i ; " ^ " ; i ; " = " , i ^ i
40
let k = k + i ^ i
50
next i
60
print " Sum( " ; j ; " ) = " , k
70
end
;
10
demo1
1
^ 1 = 1
2
^ 2 = 4
3
^ 3 = 27
4
^ 4 = 256
5
^ 5 = 3125
6
^ 6 = 46656
7
^ 7 = 823543
8
^ 8 = 16777216
9
^ 9 = 387420489
10
^ 10 = 1410065408 <== overflow
Sum(
10 ) = 1815136725 ok
32 bits integer is not much enough to cover 10 to the power of 10. If you
don't care overflow factor to write the program as following directly, the
answer will be incorrect.
:
test basic
10
let j = 1
20
for i = 2 to 10
30
let j = j + ( ( i ^ i ) mod 10 )
40
next i
50
let j = j mod 10
60
print j
70
end ; ok
test
5
ok
Correct
answer is 7 is not 5.
10
to the power of 10 is out of the able to represent range in 32 bits integer
system. This incorrect result must happened.
Another
possible option we can deal with is let the program do the maximum square up to
9 only. Because no matter how many power of 10, the last digit is always to be
0. We don't have to add it. This is not a formal option. If the last power
index is far more bigger than 10, trouble is still coming to this kind of
program.
Formal
option is to do analysis first. Question is asking you what is the last digit?
We are able to concentrate our attention on last digit only.
Chinese
are familiar with 9 times 9 table and used to do continuous multiplication
operation in mind for all single digital number. According to this habit, we
know that the result of continuous multiplication for an one digital number
itself will be a always fixed number or a sequence of numbers with cycled
variation. Result is depended on the multiplication times.
Similarly, program could followed such a deduction to
design. No matter how many times multiplication it did. Let us just reserve the
last digital number only, then keep going to do the rest self multiplication.
At last, our program is just accumulated all the last digits, it is able to
prevent overflow problem.
12.3
Program
:
test ( n -- ) \ maximum can up to very huge
[[
j ]] ! \ highest power is j
basic
10
let s = 0
20
for k = 1 to j \ for k
terms
30
let l = 1
40
for i = 1 to k
50
let l = ( l * k ) mod 10 \ reserve
only one last digit, after do multiplication each time
60
next i
80
let s = s + l \ summation
of all last digits
90
next k
100
let s = s mod 10 \ get the last digit of total summation
110
run s .
120
end
;
\
Program main shows out all results for the maximum power from 0 to 20
:
main ( -- )
basic
10
for p = 0 to 20
20
print " Last power = " ; p ; " last digit is "
30
run p test
40
next p
50
end ;
12.5
Execution Results
main
Last
power = 0 last digit is 1
Last
power = 1 last digit is 1
Last
power = 2 last digit is 5
Last
power = 3 last digit is 2
Last
power = 4 last digit is 8
Last
power = 5 last digit is 3
Last
power = 6 last digit is 9
Last
power = 7 last digit is 2
Last
power = 8 last digit is 8
Last
power = 9 last digit is 7
Last
power = 10 last digit is 7 <== the answer of this
question is here.
Last
power = 11 last digit is 8
Last
power = 12 last digit is 4
Last
power = 13 last digit is 7
Last
power = 14 last digit is 3
Last
power = 15 last digit is 8
Last
power = 16 last digit is 4
Last
power = 17 last digit is 1
Last
power = 18 last digit is 5
Last
power = 19 last digit is 4
Last
power = 20 last digit is 4 ok
12.5 Discussion
To replace 20 with many other vales in program main, showed that all digits
from 0 to 9 are possible to come out at the last digit position. Such a program
is still effective while power is huge.
A special instruction RUN is coming out in both of these 2 programs. RUN
has some meanings.
Originally, printing output ability of all traditional BASIC language are
limited. You are unable to print out a tied together message of a number and
some characters. When you are facing to such a difficult condition, in ABC
FORTH, RUN instruction can help you some. This performance has been showed
above.
I invented RUN instruction. Features include the inherent spirit of FORTH.
Let programs are able to grow up by RUN other words in FORTH.
(13)
13.1 Question: What is x?
13.2 Description
SQRT is not a standard word in FORTH. User has to prepare it by himself
for integer arithmetical application. Even though we are not difficult to cite
SQRT from anywhere. We'd better beware of some restrictions of using such a
general SQRT function.
Put the arithmetical expression listed above into the program directly,
certainly will give you a few wrong answers. Solution is existed and unique. We
have to seek another alternative condition to solve this problem. It is showing
in the following program.
13.3 Program
integer x
: test
basic
10 for x = 1 to 1000
20 if sqrt ( x + 15 ) + sqrt ( x ) = 15
and sqrt ( x ) * sqrt ( x ) = x then 40
30 goto 50
40 print " x = " ; x
50 next x
60 end ;
13.4 Execution results
test
x = 49 ok
13.5 Discussion
Existed solution should be a integer, makes us able to understand there
are some restrictions of using square root function SQRT in the program. In
general, only positive arguments should be taken into consideration to a square
root function. In integer domain of a FORTH system, execute SQRT, you are able
to get a closed to answer for most of all arguments. For example, arguments
from 5 to 8, their answers of SQRT, all are 2, the same as square root of 4.
This condition let us face to an extraneous root problem when we use SQRT
function to solve an algebraic equation. How can we overcome the incorrect
outcome?
Reverse checking can help us some. Let a simple reverse evaluation go together
with the original expression of logical branch condition. Then any extraneous
roots will be prevented from outcome.
To solve this question by free hand is not difficult. I'd like to prove it
by a simple program. It proved both the answer of question and the features of
ABC FORTH as well.
・Conclusion
All questions in all square blocks are copied from BRILLIANT.ORG website:
https://brilliant.org/practice/
Many question examples had been posted over there by many team workers.
You are welcome to visit. Smart enough answers for each question are appended
to each thread for reference for everybody. I must say thanks to them for
citing their materials here.
This article took me more than 12 days to prepare. I posted draft day by
day, question by question. Inevitable modification from time to time are always.
To add ABC FORTH on a traditional bare FORTH system is not difficult. It
made me daily using FORTH, sometimes as this article described.
My daily thinking today:
Every year, close to 28th February, the current Taiwan government is always sly to cheat all people with something about 228 affairs.
What does '228 affairs' mean?
After World War II, Japan surrender to China, but China government had never asked all Japanese to depart out from Taiwan. Roughly said, over that time, there were about 800 thousand Japanese resident in Taiwan still.
Kindly attitude from Chinese to Japanese had never been fed back any make sense response from Japanese all the time. Instead of such a Chinese kindness to Japanese, many terrible things happened to us in Taiwan after the time of Japan surrender to China.
It was a terrible affair occurred in Taiwan on 28th February 1947. Many successor of Japanese and their stupid follower, communists, and a lot of rubbish people made a comprehensive turmoil in Taiwan.
During the turmoil period of time, there were many people, they are come from Mainland China later, had been killed randomly. Turmoil people robbed weapons from army, occupied government's building as well.
Under such a situation, China government had no choice, military suppress happened, about 600 Taiwanese turmoil people were killed on site in those turmoil affairs, and more than thousand uncountable people come from Mainland China later were killed by turmoil Taiwanese.
The current Taiwan government are organized by folks pigs of Japanese. They used cheating method in national election took over the government. For the present in Taiwan, talking about the people come from Mainland China had been killed in 228 affairs in public site are prohibited. But those 600+Taiwanese victim family of 228 affairs had got huge compensation money from government already. Some of them are pseudo victims.
This is the true fact of 228 affairs in Taiwan.
Let's tell one true thing had ever happened in 228 affairs.
One person name Liu Chin San. In 1947, he was one of the people come from Mainland China later in Taiwan.
Before 228 affairs, he was one staff worked for a government company to manage exclusive cigarette and liquor.
After 228 affairs happened, one day, he had been hurt under a horrible condition, and had been sent to hospital in Taichung city.
The following day, those hurt Liu's turmoil Taiwanese heard that Liu didn't died and still alive in the hospital. Those turmoil Taiwanese rushed to the hospital immediately and killed Liu in the ward with more terrible actions, cut his ears down and dug his eyes out.
This terrible thing had ever been reported on many newspaper. And there was still a government file recorded that government company had ever arranged Liu's funeral ceremony.
The current Taiwan government would like to cheat everybody with something about 228 affairs. I'd like to tell something of the truth to all of the world.
228 affairs was an interior affairs of China government dealt with Taiwan turmoil. It was not a terrorists attacked events.
二二八真相
二二八期間,台中瘋狂打殺外省人,公賣局專员劉青山被打成重傷住院。第二天暴徒聽說劉青山没死,他们衝到病床前把劉青山打死。割掉耳鼻,挖掉双眼。
劉青山案相關挡案很多,许多报纸报導外,挡案中还有公卖局替劉青山辨公祭的资料。
三月二十五号,台湾已經平静,但是不少外省人夜宿碼頭急着逃離台湾,可見外省人惊恐到什麽程度。
民進党天天吵着要真相,现在我㑹不停地告訴你們真相。
Announcement to all of the world:
Everybody should know the real historical fact. The territory of Japan should be shrunken to three islands as the following map displayed.
In historical fact, more than 36 sequential islands of Okinawa was Chinese territory originally,
American did the bad arrangement on purpose, let it occupied by Japanese after World War II.
There was a nation organized by the aboriginal people named Ar-yi-nu kingdom on whole Hokkaido island.
Japanese killed almost all aboriginals on this island and occupied it.
附註 : 20241031 重新整理後貼出。
訂閱:
意見 (Atom)